피보나치 수와 파도반 수열
동적계획법 알고리즘 마인드를 떠올리기 힘들면 피보나치 수열, 파도반 수열을 떠올려 보자.
재귀함수와 dp의 관계: Memoization Top-down
재귀함수와 dp의 관계는 "비교 대상이자 구현법"이다.
따라서 dp의 특성을 파악하기 위해 먼저 재귀함수에 대한 이해가 필요하다.
재귀함수는 아래와 같은 그림을 기억해두면 이해하기 훨씬 수월하다! 한동안 재귀, 백트레킹 이해를 힘들어 하고 있었는데 재귀 작동 방식과 아래 그림을 연결해서 생각해보니 훨씬 이해가 잘됐다.

재귀 구현 코드는 다음과 같다.
n = int(input())
def fibo(n) :
if n <= 2: return 1
else: fibo(n-1) + fibo(n-2)위 코드는 n = 7일 때, 다음과 같은 재귀 형태의 그림으로 작동한다.

그림에 나타나듯이 재귀형태로 구현하면 fibo(5), fibo(4)... 등등이 많이 겹친다.
따라서 복잡도도 지수곱의 형태로 나타난다.으악ㅠ O(2**n)
동적계획법의 memoization 특징을 활용하면 이러한 중복된 연산 없이 답을 구할 수 있다.
n = int(input())
m = [-1 for _ in range(n+1)]
def fibo(n):
# 이미 n번째 값을 구해서 저장해둠. => memoization
if m[n] != -1: return m[n]
elif n <= 2 : return 1
else: m[n] = fibo(n-1) + fibo(n-2)
return m[n]- memoization을 이용하기 위해서는 -1로 초기화를 한 배열에 메모를 한다. -1으로 설정한 이유는 연산의 결과가 -1이 될 수 없기 때문에 조건문에서 이를 활용한다.
- 따라서 만약 m[n] 값이 -1이 아닌 경우는 이미 n 번째 값을 구해두었다는 뜻으로, 재귀함수를 호출하지 않는다.
- n = 7일 때 아래와 같이 작동한다.
- 이미 계산한 값은 memo 배열을 활용하기 때문에 연산의 횟수가 확 줄어든다. 복잡도 = O(n)
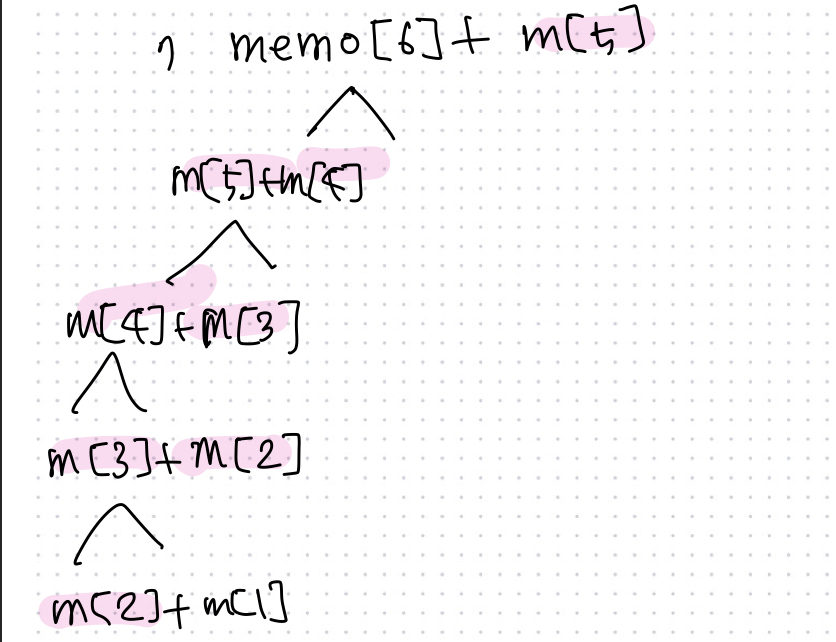
파도반 수열 재귀 구조
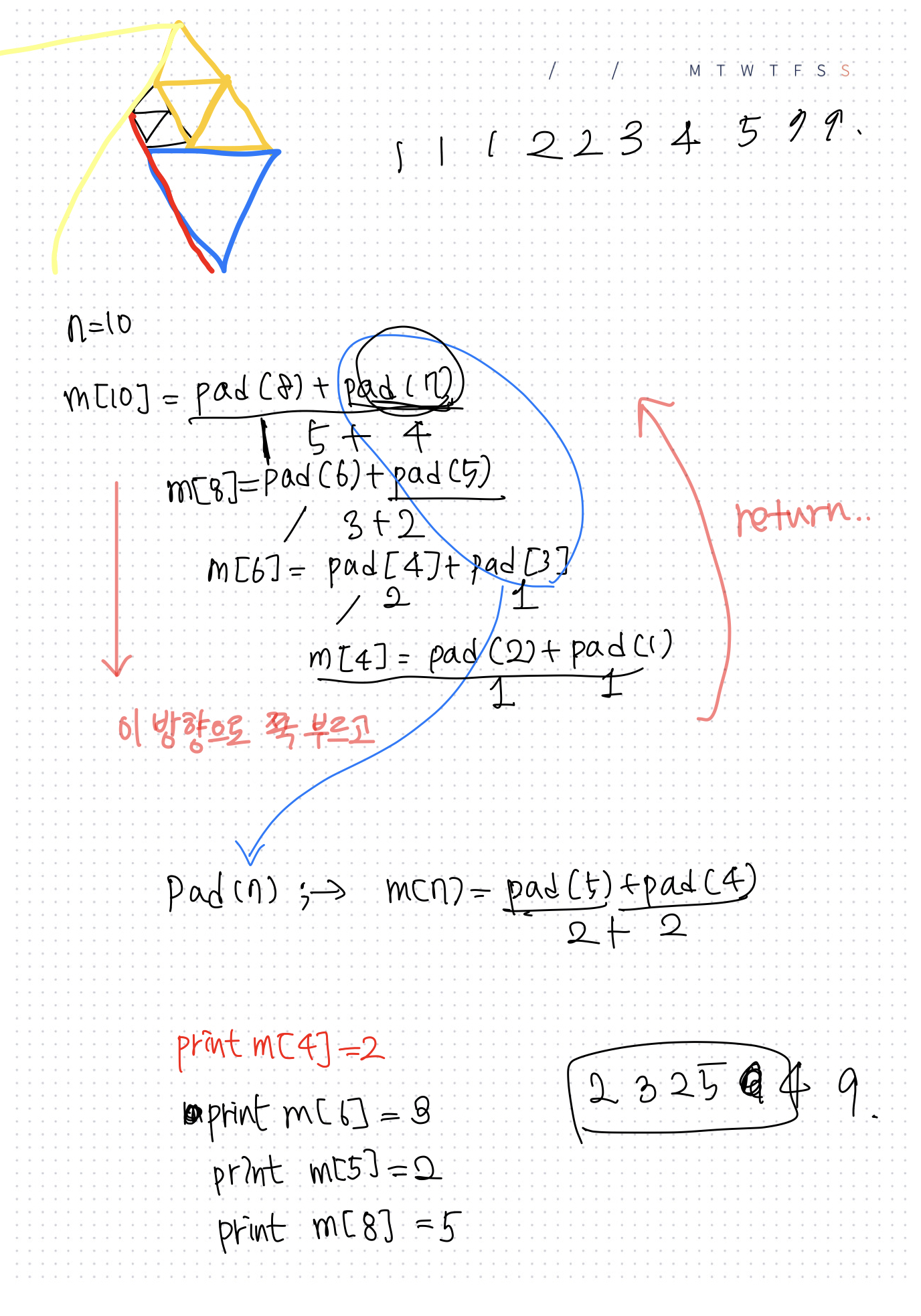
for문과 dp의 관계: Tabulation Bottom-up
앞서 재귀함수를 통해 동적 계획법을 작성하였다. 평소에 더 익숙한 배열과 for문을 이용하는 방식에 대해 알아보자.
n = int(input())
dp = [0 for _ in range(n+1)]
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
print(dp[n])Top-down? Bottom-up?
Memoization의 경우는 n번째식을 구하기 위해 n-1, n-2... 번째 값을 구하러 내려가는 재귀형식이다. 이를 탑다운 방식이라고 한다. Tabulation의 경우에는 아래서부터 값을 채워나가기 때문에(배열 왼->오 형태로) 바텀업 방식이다.
dp 문제 유형
- subtask를 그냥 합치면 되는 경우 - 타일 채우기 등
- 격자 안에서 한 칸씩 전진하는 경우
- 조건에 맞게 선택적으로 전진하는 경우
- 아이템 선택
- 문자열 매칭
Reference
코드트리 > 자료구조, 알고리즘 > 동적 계획법
코알라 기초 대면스터디
'PS > Algorithm' 카테고리의 다른 글
| [Algorithm] 이중 포문 조정 - 구간합 (1) | 2024.04.17 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (3) | 2023.06.07 |
| [알고리즘] Segment Tree (1) | 2023.04.28 |
| [알고리즘] 이진탐색 Lower/Upper Bound | Python bisect (0) | 2023.02.20 |