알파벳
오랜만의 백준 포스팅!!
코테에서 부족함을 절실히x99 느끼고 다시 알고리즘을 본격적으로 시작했다..🥲🤗
알고리즘
말이 보드를 탐색하는 조건은 다음과 같다.
① (1,1)부터 탐색한다.
② 지금까지 지나온 모든 칸에 적혀있는 알파벳과 달라야 이동할 수 있다.
이 조건 아래에서 가능한 경로 중 최대한 큰 수를 구하는 것이 목표다.
따라서, DFS를 통해 탐색하는 방법을 선택했다.
def dfs(y,x,cnt):
visited[y][x] = True
alphabet[ord(graph[y][x])-65] = True
# print('시작점: ', graph[y][x])
# 현재 위치에서 네 방향의 위치 확인
for dy, dx in dr:
ny, nx = y+dy, x+dx
if 0 <= ny < r and 0 <= nx < c :
alpha = graph[ny][nx]
#print('탐색 과정: ', alpha, " 좌표: ", ny,nx)
if not alphabet[ord(alpha)-65]:
visited[ny][nx] = True
alphabet[ord(alpha)-65] = True
cnt = dfs(ny,nx,cnt+1)
return cnt
DFS는 모든 경로에 대해서 깊이 있는 탐색을 한다. 하지만 도착지점이 중복되면 다른 경로는 탐색하지 않는다.
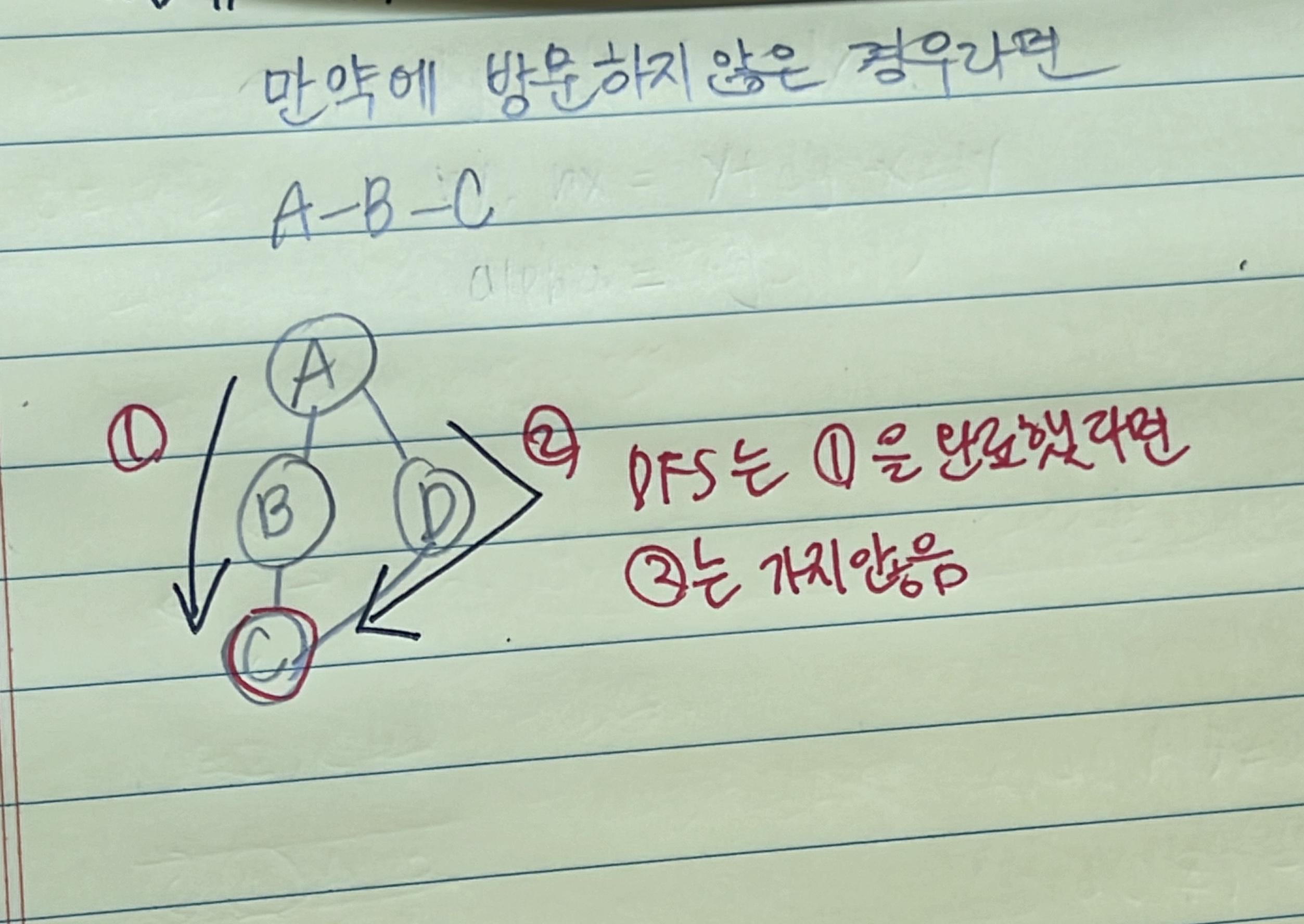

① A-B-C, ② A-D-C 경로 중에 ①이 먼저 탐색되면 ②는 탐색하지 않는 것이다.
반면에 백트래킹은 방문 시도 - 재귀 탐색 - 방문 해제 이 과정을 거쳐서, 목적지 노드가 중복되더라도 여러 경로를 탐색한다.
- DFS는 모든 노드를 최대한 깊게 탐색하지만, 목적지가 중복되는 경로라면 하나의 경로만 탐색함 => O(V+E)
- 백트래킹은 3단계를 통해서 여러 노드를 탐색한다. (각 단계마다 최선의 선택) => O(2^V)
이 문제는 탐색 문제인데도 범위가 낮은 이유가 있엇다..! 이걸 보고 백트래킹으로 최장경로를 탐색한다고 유추할 수 있으면 좋았을 것..

전체 코드
from sys import stdin, setrecursionlimit
setrecursionlimit(3000)
input=stdin.readline
r,c = map(int, input().split())
graph = [input().rstrip() for _ in range(r)]
alphabet = [False] * (ord('Z')-ord('A')+1)
dr = [(1,0),(-1,0),(0,1),(0,-1)]
max_cnt = 0
def dfs(y,x,cnt):
global max_cnt
alphabet[ord(graph[y][x])-65] = True
max_cnt = max(max_cnt, cnt)
for dy, dx in dr:
ny, nx = y+dy, x+dx
if 0 <= ny < r and 0 <= nx < c :
alpha = graph[ny][nx]
if not alphabet[ord(alpha)-65]:
alphabet[ord(alpha)-65] = True # 노드 방문
dfs(ny,nx,cnt+1) # 재귀 탐색
alphabet[ord(alpha) - 65] = False # 방문 해제!
dfs(0,0,1)
print(max_cnt)
여기서도 DFS에서는 cns를 누적하고, return 하는 식으로 구현했는데 백트래킹은 탐색하는 경로마다 max값을 찾아주는 식으로 구현을 수정했다. 또한 좌표 자체에 대한 방문 체크 대신 alphabet 방문 체크만 잘 해주면 되니까 좌표 방문 체크는 없애주었다.
알게된 점
- 백트래킹 - DFS 차이
- 백트래킹으로 최장경로 찾기 ➡️ 이게 DFS로 안 되는 이유
'PS > BOJ&Programmers' 카테고리의 다른 글
| [백준/1158] 요세푸스 문제 | 파이썬 연결리스트 | N번째 원소 (0) | 2025.02.13 |
|---|---|
| [백준/1547] 공 | 두 수의 전환 (0) | 2024.07.05 |
| [백준/1063] 킹 | 구현 실수 방지를 위한 경우의 수 체크하기 (0) | 2024.03.31 |
| [백준/5671] 호텔 방 번호 | 중복값 개수 세기(딕셔너리와 SET) (0) | 2024.03.17 |
| [백준/1068] 트리 (0) | 2024.03.06 |