1. 구간 l,r의 합 구하기(O(N))
2. i 번째 수를 v로 바꾸기(O(1))
⇒ 총 시간 복잡도는 O(NM) + O(M) = O(NM)
segment tree를 써야 하는 이유
이때 구간합 알고리즘 사용해서 앞에서부터 차례대로 합을 구해놓는 방식으로 풀 수 있음.
여기서 2번 연산을 하려면 수가 바뀔 때 마다 prefix_sum 배열을 변경해줘야 한다. 가장 앞에 있는 0번째 수가 바뀐다면 모든 prefix_sum 배열을 변경해야 하기 때문에 시간 복잡도는 O(N)
따라서, M과 N이 매우 큰 경우에는 결국..! 시간 초과.
세그먼트 트리를 사용하면 O(N) → O(lg N), O(M) → O(lg N)
정의
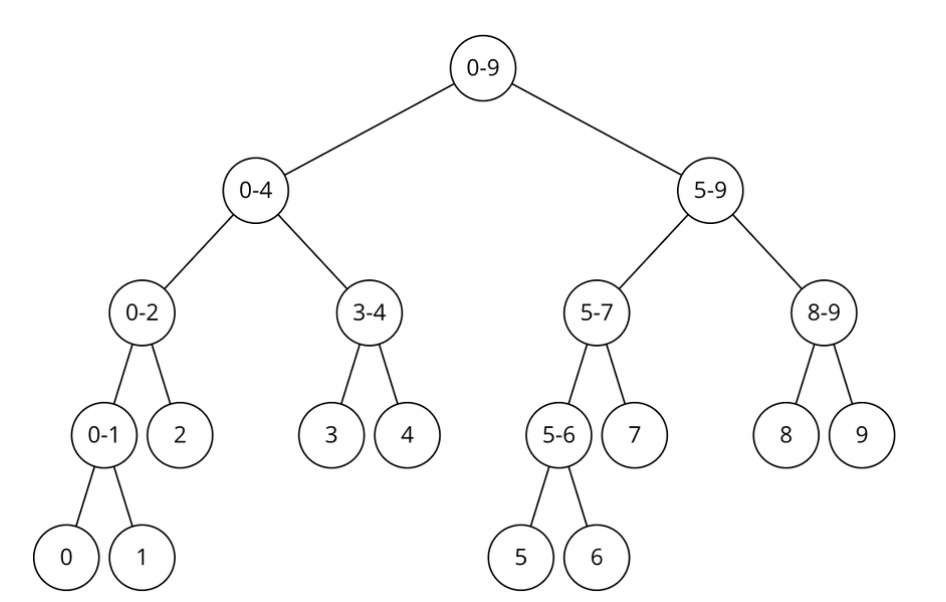
리프 노드를 제외한 다른 모든 노드는 항상 2개의 자식을 가진다.
⇒ Full Binary Tree의 형태.
- 리프 노드: 배열의 그 수 자체
- 다른 노드: 왼쪽 자식과 오른쪽 자식의 합
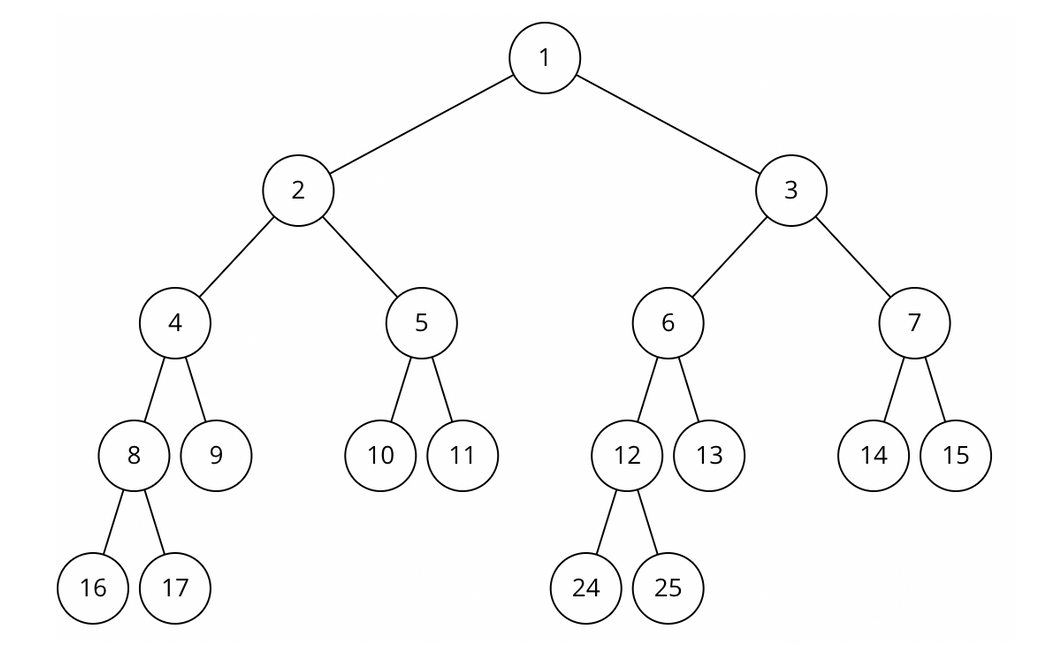
- 어떤 노드의 번호가 x일 때 왼쪽 자식의 번호는 2x, 오른쪽 자식의 번호는 2x+1.
구현 방법
'''
a: 배열 A
tree: 세그먼트 트리
node: 노드 번호
node에 저장되어있는 합의 범위: start - end
'''
def init(a, tree, node, start, end):
if start == end : tree[node] = a[start]
else:
init(a, tree, node*2, start, (start+end)//2) # 왼쪽 자식
init(a, tree, node*2+1, (start+end)//2+1, end) # 오른쪽 자식
tree[node] = tree[node*2] + tree[node*2+1]
node 구간: [start, end]
왼쪽 자식: [start, (start+end)//2]
오른쪽 자식: [(start+end)//2+1, end]
세그먼트 트리_구간합 구하기(query)
- [left,right]: 구해야 하는 합의 범위
- [start,end]: node에 저장된 구간
구간 left, right가 주어졌을 때 합을 구하려면 트리를 루트부터 순회, 각 노드에 저장된 구간의 정보와 left, right와의 관계
1. [left, right]와 [start, end]가 겹치지 않는 경우
if (left > end or right < start)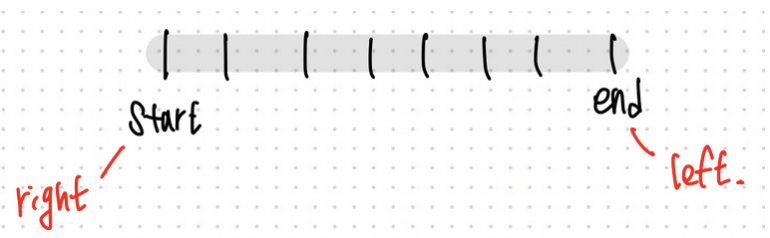
→ 아예 겹치지 않으니까 탐색 필요 x, return 0 탐색 중단2.
2. [left,right]가 [start,end]를 완전히 포함하는 경우
if (left <= start and end <= right)
→ 겹치지 않는 범위도 모두 포함되기 때문에 return tree[node]
3. [start,end]가 [left, right]를 완전히 포함하는 경우, 겹친 경우 ➡️ 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작
def query(tree, node, start, end, left, right):
# 아예 겹치지 않음
if left > end or right < start: return 0
if left <= start and end <= right: return tree[node]
lsum = query(tree, node*2, start, (start+end)//2, left, right)
rsum = query(tree, node*2+1, (start+end)//2+1, end, left, right)
return lsum + rsum
세그먼트 트리_수 변경하기(update)
✔️ idx 번째 수를 val로 변경하는 경우, idx 번째를 포함하는 노드에 들어있는 합까지 변경해주어야 한다.(왼/오 자식에 따라서 누적합을 나눠서 저장했으니까)
- 원래 idx 수 = li[idx]
- 바뀐 수가 val이라면 합은 val - li[idx]만큼 변한다.
수 변경 상황 가정
- [start,end]에 idx가 포함되는 경우 ⇒ 재귀 호출 진행해서 값 구하기
- [start,end]에 idx가 포함되지 않는 경우 ⇒ 재귀 호출 중단
문제
import sys
from math import ceil, log2
input = sys.stdin.readline
n,m,k = map(int, input().split())
li = [int(input()) for _ in range(n)]
# 세그먼트 트리 초기화
h = ceil(log2(n))
tree = [0]*(1 << (h+1))
def init(li, tree, node, start, end):
if start == end : tree[node] = li[start]
else:
init(li, tree, node*2, start, (start+end)//2)
init(li, tree, node*2+1, (start+end)//2+1, end)
tree[node] = tree[node*2]+tree[node*2+1]
def query(tree, node, start, end, left, right):
if left > end or right < start: return 0
if left <= start and end <= right: return tree[node]
lsum = query(tree, node*2, start, (start+end)//2, left, right)
rsum = query(tree, node*2+1, (start+end)//2+1, end, left, right)
return lsum+rsum
def update(li, tree, node, start, end, idx, val):
if idx < start or idx > end: return
# 리프 노드를 찾을 때까지 계속 재귀 호출 이어나가는 방법
if start == end:
li[idx] = val
tree[node] = val
return
update(li, tree, node*2, start, (start+end)//2, idx, val)
update(li, tree, node*2+1, (start+end)//2+1, end, idx, val)
tree[node] = tree[node*2] + tree[node*2+1]
init(li, tree, 1, 0, n-1)
# a=1 값 변경, a=2 sum(li[a]:li[b+1])
for _ in range(m+k):
a,b,c = map(int, input().split())
if a == 1:
update(li, tree, 1, 0, n-1, b-1, c)
else:
print(query(tree, 1, 0, n-1, b-1, c-1))
Reference
https://book.acmicpc.net/ds/segment-tree
세그먼트 트리
누적 합을 사용하면, 1번 연산의 시간 복잡도를 $O(1)$로 줄일 수 있습니다. 하지만, 2번 연산으로 수가 변경될 때마다 누적 합을 다시 구해야 하기 때문에, 2번 연산의 시간 복잡도는 $O(N)$입니다.
book.acmicpc.net
'PS > Algorithm' 카테고리의 다른 글
| [Algorithm] 이중 포문 조정 - 구간합 (1) | 2024.04.17 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (3) | 2023.06.07 |
| [알고리즘] convex hull(컨벡스 헐) (1) | 2023.05.02 |
| [알고리즘] 헷갈려서 정리해보는 DP 🙀 | 재귀 - Memoization | for 배열 - Tabulation | Top-down & Bottom-up | 문제 유형 (0) | 2023.04.17 |
| [알고리즘] 이진탐색 Lower/Upper Bound | Python bisect (0) | 2023.02.20 |