알고리즘
이 문제는 완전탐색 방식으로 풀면 점의 개수가 1000 개일 때, 1000 * 1000 * 1000 = 10^9로 시간 초과를 하게 된다.
따라서 세 점의 거리가 동일한 케이스를 모두 계산하는 방법이 아닌, 동일한 간격이 존재하는 점을 찾는 방식으로 구현하도록 한다.
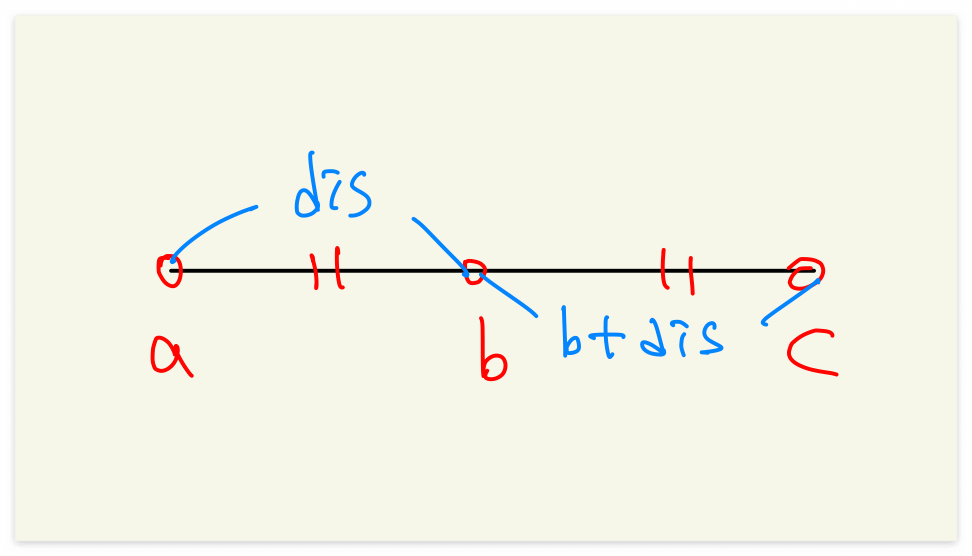
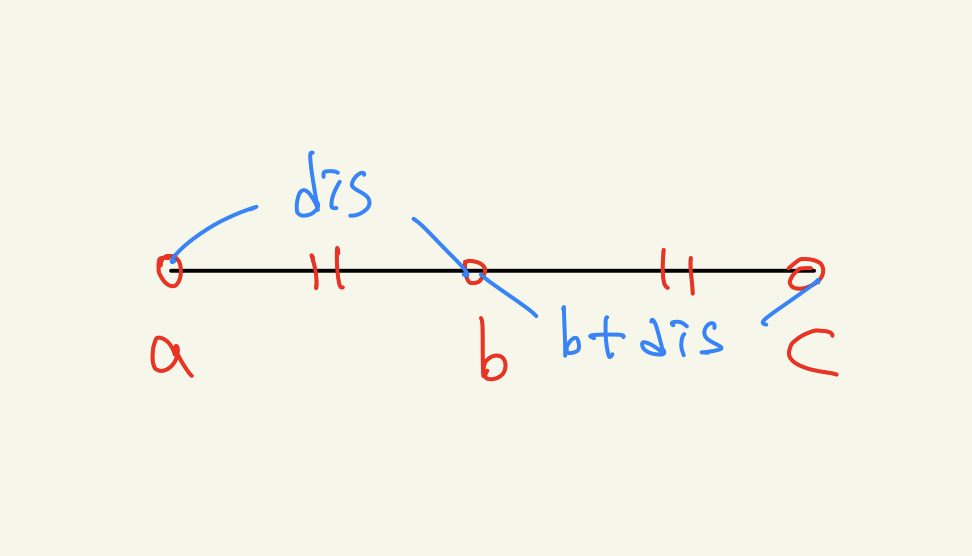
수직선 상에 임의의 세 점 a,b,c가 있을 때 점 C는 b에서 a와 b의 거리만큼 더한 값이다.
이 알고리즘을 활용하여 점 C를 찾고, 이 값이 입력받은 list에 존재한다면 세 점은 동일한 거리를 가진 점들이다.
최종 코드
from collections import defaultdict
t = int(input())
for _ in range(t):
n = int(input())
dots = sorted(list(map(int, input().split()))) # 점 입력 받고 sort
spot = defaultdict(int)
for i in range(n):
# 점의 위치를 key 값으로 존재하면 1 (True)
spot[dots[i]] = 1
print(spot)
ans = 0
for i in range(n-1):
for j in range(i+1, n):
# 세번째 점은 첫번째 점과 두번째 점 거리값과 동일
third = dots[j] + (dots[j] - dots[i])
if spot[third] == 1:
ans += 1
print(ans)
점의 존재 여부를 확인하기 위해 defaultdict를 사용했다.
defaultdict는 dictionary의 서브 클래스로 key값 또한 디폴트로 자료형을 선언할 수 있다.
for문의 범위는 첫번째 값으로부터 두번째 값까지의 거리를 모드 계산해주기 위해 위와 같이 설정한다.
이 값이 defaultdict에 존재하면 개수를 세어준다.
'PS > BOJ&Programmers' 카테고리의 다른 글
| [백준/4949] 균형잡힌 세상 | Stack (0) | 2023.01.21 |
|---|---|
| [백준/14592] 2017 아주대학교 프로그래밍 경시대회(small) - 파이썬 (2) | 2023.01.18 |
| [백준/12759] 틱! 택! 토! - 파이썬 (1) | 2023.01.17 |
| [백준/1100] 하얀 칸 | 파이썬 2차원 리스트 (0) | 2023.01.16 |
| [백준/11652] 카드 - 파이썬 (0) | 2023.01.14 |